Introduction
In the oil and gas industry, the reliability of instrumentation equipment and industrial
control systems is fundamental to ensuring operational continuity, process safety, and the
profitability of operations. Maintaining these assets requires a strategic and structured
approach, especially in a sector where the margin for error is minimal and the consequences
of failure can be catastrophic. In this context, Reliability-Centered Maintenance (RCM)
becomes an essential tool.
The SAE JA1011 standard establishes clear and specific
criteria for evaluating RCM processes, proposing a set of “7 questions” that guide the
implementation of this methodology. These questions allow maintenance and reliability managers
to effectively identify and manage failure risks, establishing preventive and predictive
maintenance strategies that optimize resources and maximize the lifespan of assets.
The
SAE JA1012 standard provides a detailed explanation of the essential criteria guiding the
answers to the “7 questions”, defining the necessary requirements for evaluating RCM processes
and identifying additional elements that must be considered to ensure effective
implementation. This offers a comprehensive framework for those who wish to rigorously and
successfully apply the RCM methodology.
In this article, I aim to explore each of the
“7 RCM questions” from the perspective of instrumentation and control systems applied to the
oil and gas production industry, a field in which I have developed my professional career.
Throughout this analysis, I will share examples and reflections based on my direct experience
in designing and implementing maintenance plans. This practical approach will enable readers
to visualize how the principles of the SAE JA1011 standard, in conjunction with the SAE JA1012
standard, can be applied in critical industrial environments, helping to prevent unplanned
downtime, optimize safety, and reduce operational costs.
The intention of this article
is to provide a structured and practical guide that enables professionals in the sector to
develop robust maintenance plans tailored to the specific needs of the oil and gas industry.
By applying RCM principles, maintenance teams can significantly improve the reliability and
performance of assets, ensuring safer and more efficient operations.
What are the desired functions and associated performance standards of the asset in its
current operational context (functions)?
To implement Reliability-Centered Maintenance (RCM) on instrumentation equipment and
industrial control systems within the oil and gas sector, it is essential to clearly
understand the desired functions of each asset and the performance standards it must meet in
its operational context. In this industry, these systems play a critical role in ensuring
that processes remain stable, efficient, and, above all, safe. Any deviation in their
operating parameters can jeopardize operations and lead to significant financial losses.
The first step in developing any maintenance plan, which aligns with section 5.1.1 of the
SAE JA1011 standard, is a demanding and highly responsible task. Defining the operational
context of each asset requires searching, collecting, and connecting the documentation related
to the project's design and construction, particularly for new equipment or projects. For
assets or projects already in operation, this process also necessitates access to operational
history.
Based on my professional experience, the documentation I have used as input
for defining the operational context applicable to instrumentation and control systems is
illustrated in Figure 1. This initial step also requires effective, multidisciplinary
communication with the organizational departments involved in project development or
operation, in conjunction with the application of international, national, regional, and
company-specific standards.
This is because the functions and failure management
strategies of an asset are influenced not only by the asset itself but also by the context in
which it operates. Therefore, a clear definition of the operational context is essential
before addressing questions related to asset performance and reliability.
A
description of how instrumentation and control systems are intended to be used in a specific
project, the geographical and environmental conditions where these systems will operate, along
with standards related to production, performance, safety, and environmental integrity, are
the required components for declaring an operational context.
In Figure 1, it can also
be observed that the output of the operational context declaration is a document that
identifies whether the instrumentation and/or control system will operate in a batch
(intermittent) or flow (continuous) process, the expectations for product quality and
customer service, including metrics such as waste rates and customer satisfaction, and
compliance with relevant environmental regulations at organizational, regional, national, and
international levels.
Additionally, the document declaring the operational context
must identify established safety expectations, including injury and fatality rates, the
characteristics of the operational environment (e.g., arctic or tropical), the operational
schedule (e.g., continuous or intermittent), and load conditions (maximum load or base load),
as well as the availability of backup systems or capacities.
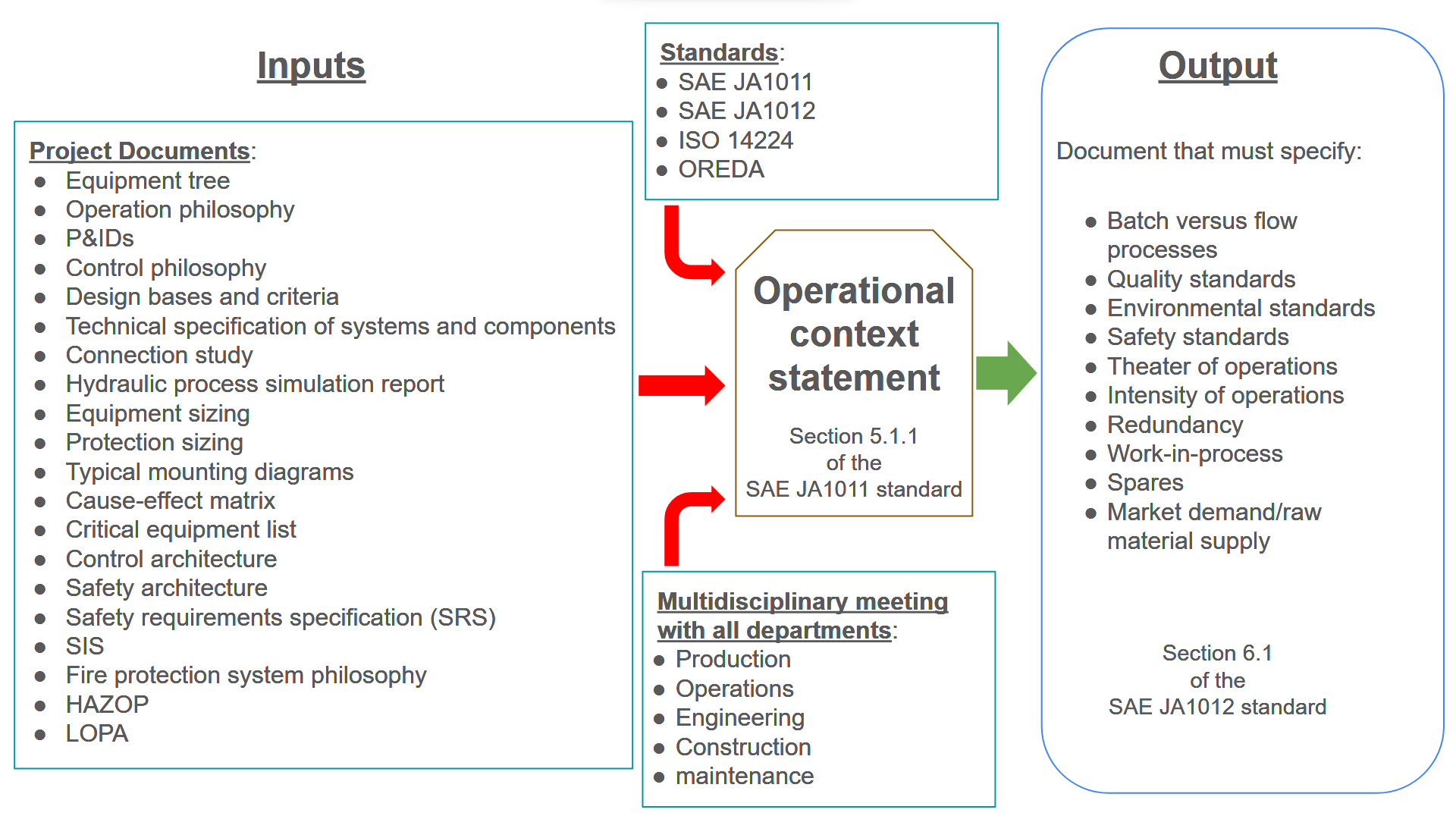
Figure 1. Scheme based on the operational context criteria and guidelines described in
SAE JA1011 and SAE JA1012 standards.
It should also identify the extent to which work in progress can absorb equipment downtime
without affecting total production, decisions on the storage of critical spare parts that may
influence failure management strategies, and consideration of market demand fluctuations and
raw material availability that could impact operations.
For complex systems, it may be
beneficial to organize the operational context hierarchically, beginning with the
organization's general mission statement that uses the asset.
Instrumentation assets
in oil and gas fulfill desired or required functions such as accurately measuring variables
(pressure, temperature, flow, etc.), continuously monitoring processes, and generating
control signals that enable real-time automatic adjustments. On the other hand, control
systems (such as DCS or PLCs) interpret signals from instruments and adjust operations to
maintain conditions within safe and operational limits.
According to section 5.1.2 of
the SAE JA1011 standard, the functions to be identified are classified into primary and
secondary functions. Primary functions are the fundamental reasons an organization acquires
an asset or system. These functions represent the core purpose of the asset or system and are
essential to achieving the organization’s objectives.
For example, consider a
transmitter that measures level by differential pressure. The LIT-0715012 asset fulfills the
following primary functions:
-
Measuring the level in the Clarifier Tank CLFT-071692.
-
Transmitting the control signal to the PLCINS-018270 controller located in the
Control Cabinet PLCSTAP-018270.
-
Activating interlock I3 for high level in the Clarifier (H = 112.58 inH2O),
triggering the closure of valve FCV-071910 to prevent production water from entering
the Clarifier from the Fwko Tanks (TK-071011/2) and the Washing Tanks (TK-071293/4).
-
Activating interlock I8 for low level in the Clarifier (L = 104.59 inH2O), triggering
the closure of valve XV-0716021 to prevent sludge from leaving the Clarifier toward
the distribution header feeding the Sludge Pumps AP-071601A/B.
According to section 6.2.1 of the SAE JA1012 standard, this means the transmitter must:
-
Measure level: The primary function is to measure water level in the clarifier
tank, which is the central purpose of having a level transmitter.
-
Measurement capacity: The transmitter must measure levels via differential
pressure within a range of 104.59 inH2O to 112.58 inH2O, implying appropriate design
and mounting space.
-
Alarm activation: The references to "104.59 inH2O" and "112.58 inH2O"
establish performance standards in terms of differential pressure, which are critical
for the transmitter’s functionality in level measurement.
Identifying primary functions is crucial for several reasons:
-
Performance Focus: Enables the organization to focus on the asset's
performance to meet objectives.
-
Maintenance Strategy Development: Understanding primary functions helps
establish maintenance policies to ensure the asset continues to fulfill its purpose.
-
Risk Assessment: Understanding primary functions allows for identifying risks
associated with their failure and developing mitigation strategies.
-
Investment Justification: Demonstrates how the asset contributes to
organizational objectives, justifying its acquisition.
Secondary functions, according to the SAE JA1012 standard, are additional functions performed
by the asset. These are generally less apparent than primary functions but, depending on the
asset's operational context, the loss of one or more secondary functions can significantly
impact overall performance and operability, sometimes even more so than the loss of primary
functions.
For the differential pressure level transmitter, secondary functions
include containing production fluids and auxiliary liquids in the process connection.
Secondary functions require as much attention as primary ones since they can influence
safety, efficiency, and user satisfaction. It is crucial to ensure they are clearly
identified.
Another example involves a control cabinet. Its secondary functions
include supplying electrical power, cooling, connectivity, structural support, and physical
space for the reliable and safe operation of the equipment housed within. It also protects
internal devices from mechanical risks (impacts, vibration, breakage, abrasion, etc.),
physical risks (humidity, solar radiation, excessive temperature, etc.), among other risks,
allowing the controller and its peripherals to operate reliably and safely under specified
environmental conditions.
When identifying secondary functions, the following aspects
should be considered, according to the SAE JA1012 standard:
-
Environmental Integrity: Ensuring the asset complies with environmental
regulations and does not harm the environment.
-
Structural/Safety Integrity: Evaluating whether the asset maintains its
structure and safety during operation.
-
Control/Containment/Comfort: Considering the asset's ability to regulate its
performance and provide a safe and comfortable environment.
-
Appearance: Aesthetic signaling of the asset, particularly in environments
where visibility and readability are necessary.
-
Protection Devices and Systems: Identifying functions that protect the asset
and users from failures or abnormal conditions.
-
Economy/Efficiency: Assessing how the asset contributes to operational
efficiency and cost control.
-
Superfluous Components: Recognizing non-value-adding components that could be
removed to improve efficiency.
It is important to emphasize that, according to section 5.1.2 of the SAE JA1011 standard, the
identification of asset functions must include the functions of all protection devices.
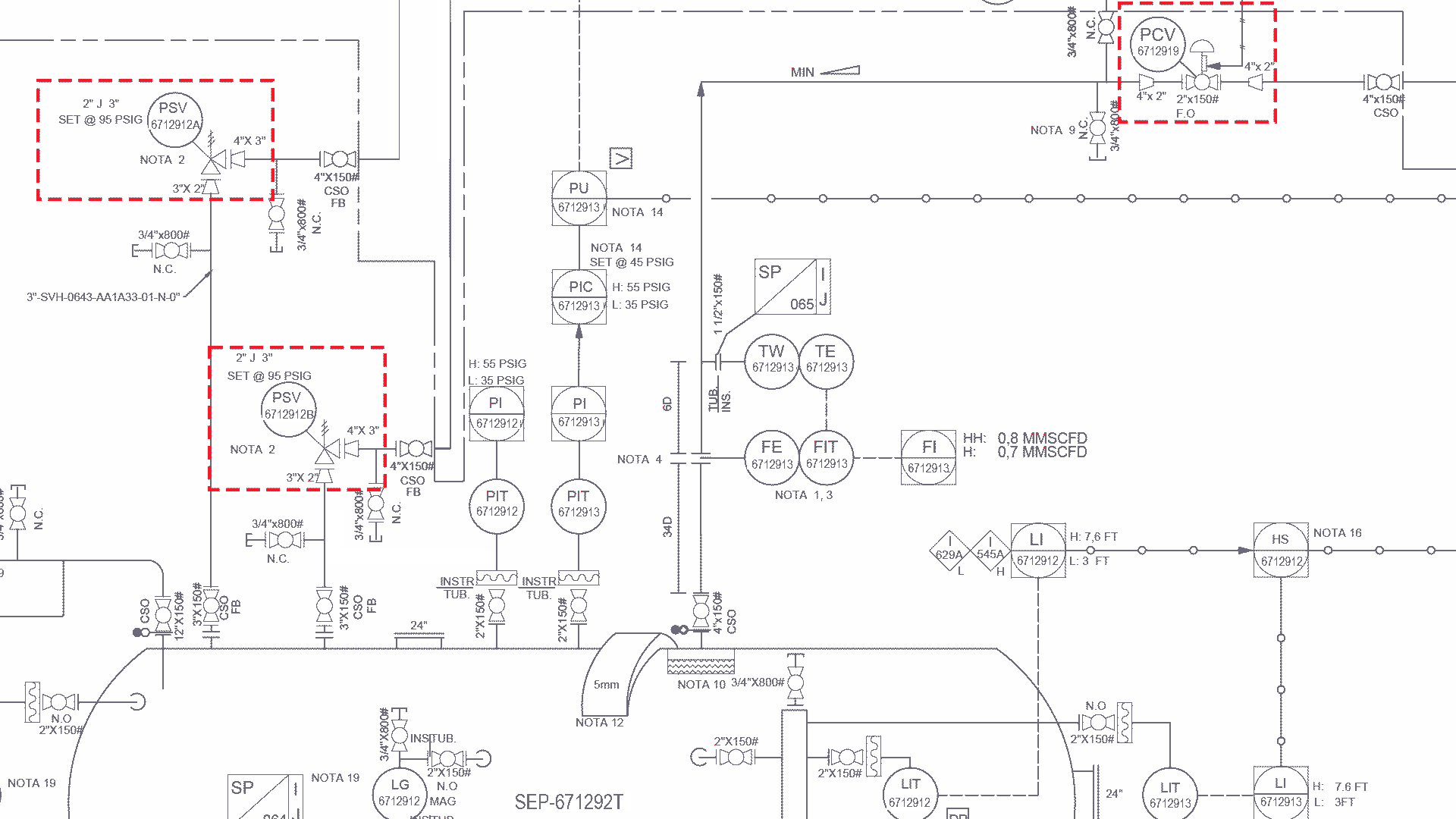
Figure 2. Functions of protection devices in the framework of the SAE JA1011 standard.
As an example, in defining the primary and secondary functions of the pressure control valve
PCV-6712919, shown in the red box in Figure 2, the functions of the pressure safety relief
valves PSV-6712912A/B must be included because they are the protection devices of the
three-phase separator SEP-671292T. These valves must open in scenarios of overpressure
associated with failures in the pressure control valve in the gas-to-flare line.
According to section 5.1.3 of the SAE JA1011 standard, the definition of each function must
include a verb, an object, and a performance standard, which should be quantified whenever
possible. This ensures that expectations regarding the asset's operation are clear and
measurable.
In the example in Figure 2, one of the primary functions of the pressure
control valve is to open proportionally to the gas pressure in the three-phase separator. A
secondary function is to contain the gas in the mechanical connection with the pipe. One of
the functions of the protection devices is to open instantaneously if the separator pressure
reaches 95 psig to relieve overpressure caused by the loss of the primary function of the gas
pressure control valve in the separator.
In the above example, the structure for
defining functions, as outlined in the SAE JA1012 standard, is applied:
-
Verb: Indicates the action the asset must perform. For example, in the case
of the proportional pressure control valve, the verb is “open”.
-
Object: The element on which the action is performed. For the valve, the
object is “gas”.
-
Performance Standard: Defines the conditions under which the function must be
performed, including specific metrics. For the valve, the performance standard is
“proportional to the gas pressure in the three-phase separator”.
-
Protection Functions: Must include the word “if” or the phrase “in case of”,
followed by a brief summary of the circumstances that will trigger the protection
function, as seen in the example of the safety relief valves mentioned in Figure 2.
In my experience, accurately identifying primary, secondary, and protection device functions
not only enables the design of more efficient maintenance plans but also helps prioritize
resources for those assets whose failure could negatively impact process safety or lead to
unplanned shutdowns.
The functions defined for the assets in the above examples also
incorporate performance standards, which are crucial to represent the level of performance
desired by the client (owner or operator) within the operational context of the asset, as
indicated in section 5.1.4 of the SAE JA1011 standard.
This includes defining
acceptable operational thresholds, measurement or response frequencies, and required
precision levels. These standards are typically derived from both manufacturer specifications
and internal industry regulations. In my experience, having these criteria clearly defined
makes it more effective to identify when an asset begins to deviate from normal behavior,
facilitating timely intervention before a failure occurs.
An asset is considered failed
when its performance drops below the minimum acceptable level defined by the client.
Conversely, if the asset maintains performance above this threshold, it is considered to be
operating satisfactorily. Users include not only owners but also operators and society, which
expects assets to operate safely and without causing environmental harm.
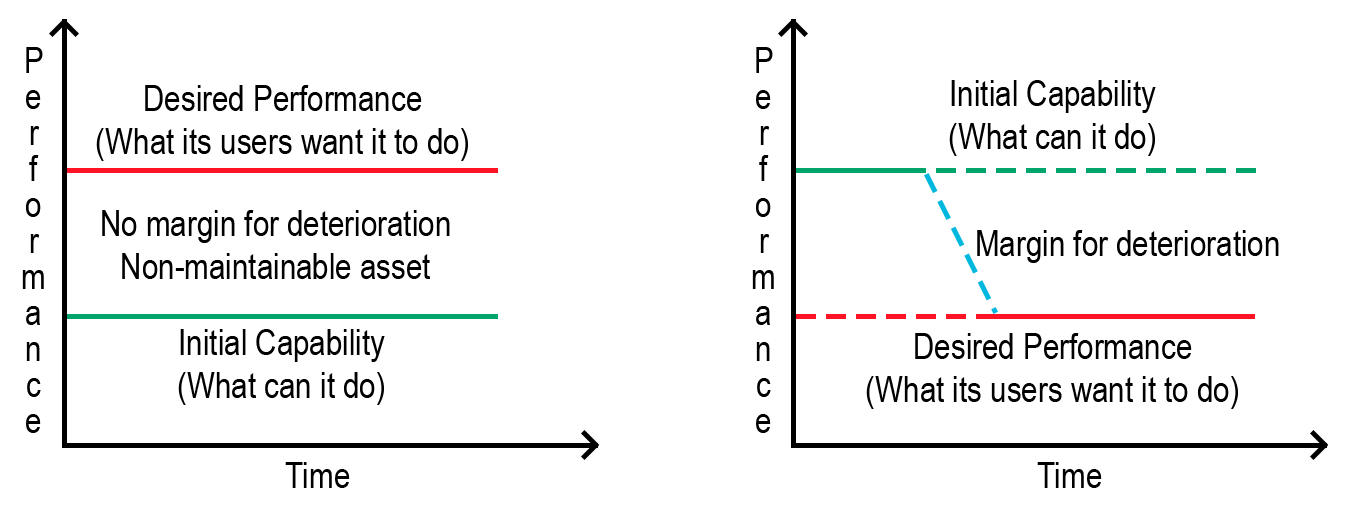
Performance
can be evaluated from two perspectives: desired performance (what users expect) and inherent
capability (what the asset can actually achieve). When commissioning an asset, its initial
capacity must exceed the minimum performance standard, as shown in the right-hand graph in
Figure 3. This ensures a margin for deterioration before the asset reaches functional failure.
The design of an asset must consider deterioration, allowing for a reasonable
performance margin. However, this margin should not be excessive, as it could result in
over-design and increased costs. If the desired performance exceeds the built-in capacity,
the asset may become unmaintainable, meaning maintenance efforts will not be sufficient to
meet user expectations, as illustrated in Figure 3.
For this reason, it is essential
to quantify performance standards whenever possible, as this ensures accuracy and precision.
In situations where qualitative standards are required (e.g., for aesthetic functions), it is
crucial to ensure these standards are clearly understood by all stakeholders involved.
Figure 3. Relationship between Initial Capacity, Margin for Deterioration, and Desired
Performance in Industrial Assets within the Framework of SAE JA1012.
Throughout my career, I have learned that understanding functions and performance standards
is not just a theoretical exercise but involves observing how each asset responds within its
operational context. Instrumentation and control systems, in particular, are exposed to harsh
environments with variations in temperature, pressure, vibration, and corrosion, which affect
their reliability over time. A good practice is to periodically review and adjust performance
standards to align with current operating conditions, especially if these change due to
facility expansion or modification.
Additionally, I have found that involving
operators and technicians in the process of defining functions and standards helps capture
specific details about asset behavior in operation. Operators, who are in direct contact with
the systems, often provide valuable insights into the sensitivity or response of certain
instruments under particular conditions. This knowledge is a significant advantage for the
maintenance team, enabling them to anticipate potential deviations and establish better
intervention strategies.
How can assets fail to perform their functions (functional failures)?
The Fourier Transform is a mathematical tool that converts a signal from the time domain to
its representation in the frequency domain. Essentially, it breaks down a complex signal
into a set of sinusoidal waves of different frequencies.
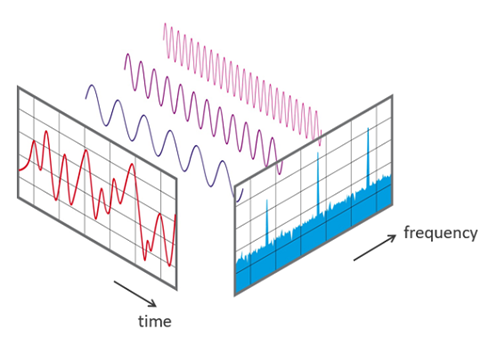
Its main application is signal analysis, allowing the identification of the dominant
frequency and essential characteristics of any continuous signal.
This is fundamental
in fields like telecommunications, where it is used for visual and audio signal processing,
in wave physics for vibration analysis, and in control systems for filtering noise in
electrical signals, among others.
The Discrete Fourier Transform (DFT) is a variant
of the Fourier Transform, adapted to work with discrete signals. As technology has advanced
towards digital systems, continuous signals have been replaced by digital signals, that is,
values taken at specific time intervals.
The DFT converts a discrete signal into a
series of frequency components, allowing the analysis of frequencies in digital systems.
Some examples of its use include analyzing the frequency of digital signals in applications
like image and audio compression, frequency detection in financial time series, and more.
Although the DFT is a powerful tool, its computational cost is high, especially for large
signals. This is where the Fast Fourier Transform (FFT) comes in, an algorithmic improvement
that significantly reduces the computation time, going from O(N²) complexity in the DFT to
O(N logN) in the FFT.
This has made signal analysis more efficient by allowing
electronic devices and computing systems to process signals much faster, making it a
cornerstone of modern technology.
In summary, while the FT is the general tool
applied to continuous signals and is useful in mathematical theory, the DFT is its discrete
counterpart used for signals in digital systems, and the FFT is an optimized algorithm to
compute the DFT efficiently, drastically reducing processing time.
Despite the
advantages of FFT, there was room to improve its performance on modern hardware. This is
where FFTW (Fastest Fourier Transform in the West) comes in.
FFTW is a highly
optimized software library for computing FFT on various hardware architectures, taking
advantage of cache memory and the specific characteristics of each system.
FFTW
achieves outstanding performance by dynamically generating optimized code at runtime,
allowing FFT calculations faster than traditional implementations.
Its appearance has
facilitated the analysis of high-frequency signals in scientific research and advanced
engineering applications, marking a milestone in FFT computation across various systems.
But what is FFTW?
FFTW, which stands for 'Fastest Fourier Transform in the West', is a widely used library for
computing the Fast Fourier Transform (FFT). Initially developed at MIT, its purpose is to
optimize FFT performance across different platforms, being adaptable to both complex and real
data, in one or multiple dimensions.
FFTW uses a unique approach known as 'planning',
where it optimizes operations for the specific hardware on which it is run, allowing the
computation to be as efficient as possible.
The efficiency of FFTW comes from its
ability to generate plans that optimize the FFT calculation. The software automatically
selects from various execution strategies, allowing it to adapt to the specificities of the
target hardware.
It uses a combination of techniques, such as recursive factorization
and redundancy elimination in the calculation, which drastically reduce the number of
operations needed compared to traditional implementations.
FFTW also takes processor
cache into account, optimizing memory usage and reducing access times, making it one of the
fastest FFT implementations.
While other FFT libraries, such as NVIDIA’s cuFFT for
GPU or Intel's FFT, are also highly efficient on specific platforms, FFTW stands out for its
ability to adapt to a wide variety of architectures and devices, optimizing performance
without manual intervention.
Unlike manual FFT implementations, which can be useful
for very specific applications but are prone to errors and rarely optimize automatically,
FFTW simplifies the process by automatically generating the most efficient strategies. Among
the key advantages of using FFTW, we can mention:
-
Portability: FFTW is compatible with a variety of platforms and operating
systems, ensuring that code using FFTW is portable and efficient across multiple
environments.
-
Automatic optimization: The developer doesn't need to manually optimize FFT
operations, as FFTW automatically generates the best plan for the hardware.
-
Versatility: FFTW supports one-dimensional and multidimensional Fourier
transformations, as well as working with complex and real signals.
-
Large community and support: FFTW is an open-source library with widespread
use in the scientific and technical community, ensuring access to documentation and
continuous support.
FFTW Implementation in C++
The implementation of FFTW in C++ follows a structured process that, although it involves
several steps, ensures an efficient and functional integration of this powerful library into
any project. Below are the essential steps to set up FFTW in a C++ environment using the
Visual Studio IDE.
-
Before starting the implementation, it's necessary to ensure that the
development environment is ready. Visual Studio must be properly installed, along
with the necessary compilers for working with C++. It is important to have a
compatible version of Visual Studio with C++ support, preferably version 2022 or
higher. Additionally, you should verify that the project is configured to work with
the appropriate architectures, such as x86 (32-bit) and x64 (64-bit).
-
The next step is to download the appropriate version of the FFTW library.
Depending on your project's architecture (32 or 64 bits), you should download the
precompiled version of the library from the official FFTW website. Versions are
available for both Windows and Linux, as well as source files if you prefer to
compile the library yourself.
-
Once the library is downloaded, if necessary, you can compile the .dll and
.lib files from the .def definition files. This is done using the
Visual Studio compiler. The compilation will generate dynamic library files
(.dll) and static libraries (.lib), which will be used in the project.
A useful command for this task in 32-bit architecture is:
lib/def:libfftw3-3.def/out:fftw3.lib/machine:x86. Whereas for a 64-bit
architecture it is:
lib/def:libfftw3-3.def/out:fftw3.lib/machine:x64.
-
To use FFTW in your project, you must include the header files (.h) and
libraries (.lib). This is done by adding the corresponding paths to the files in
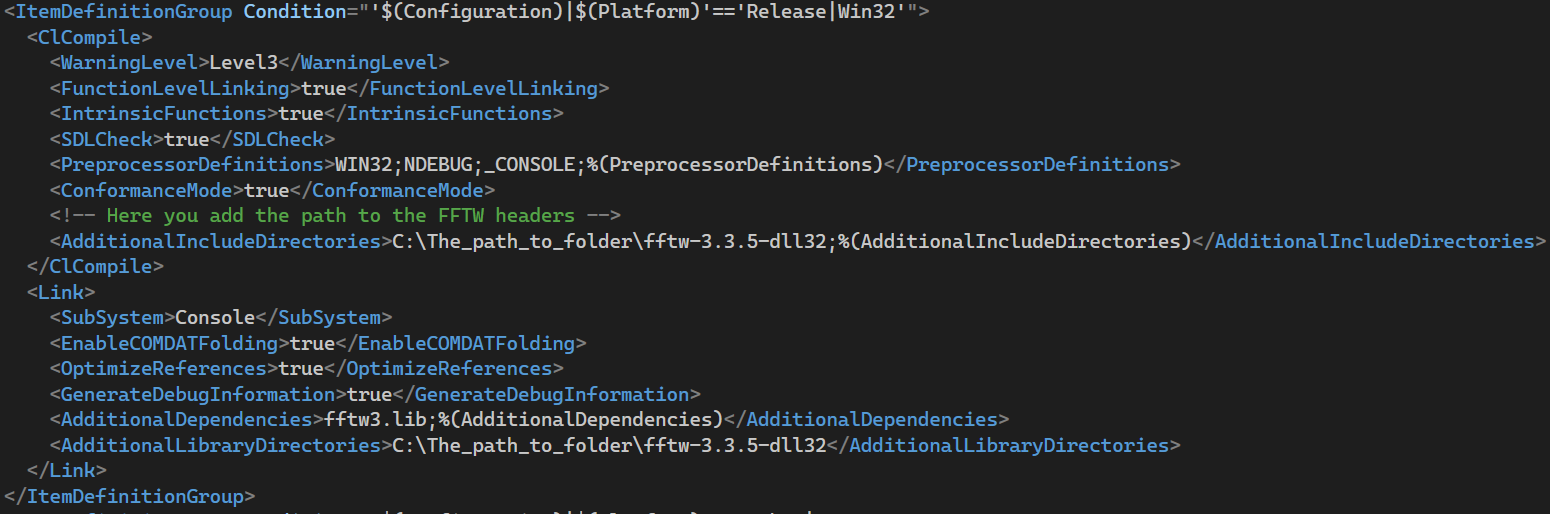
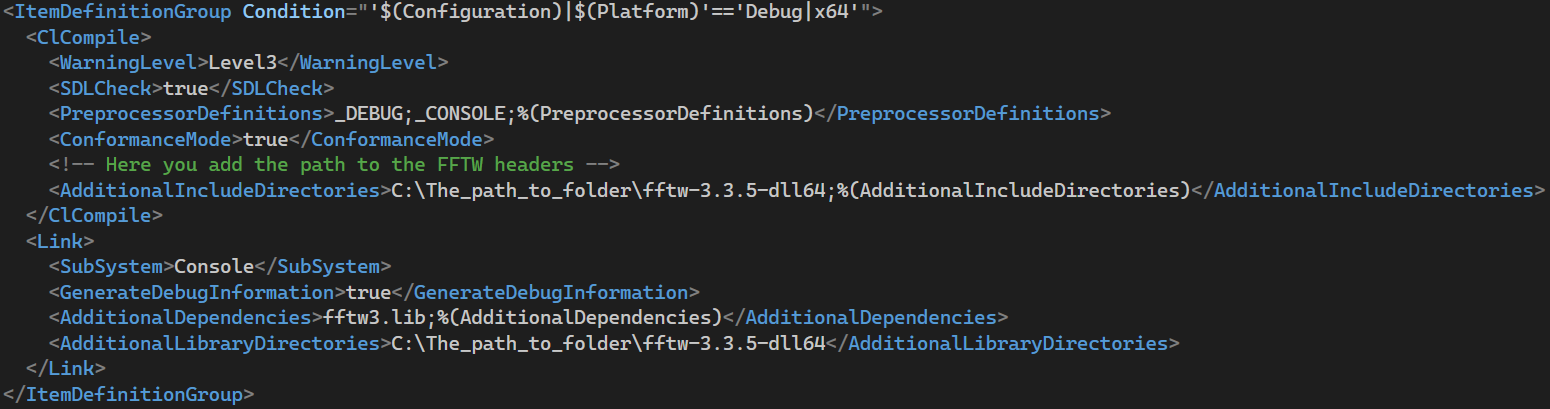
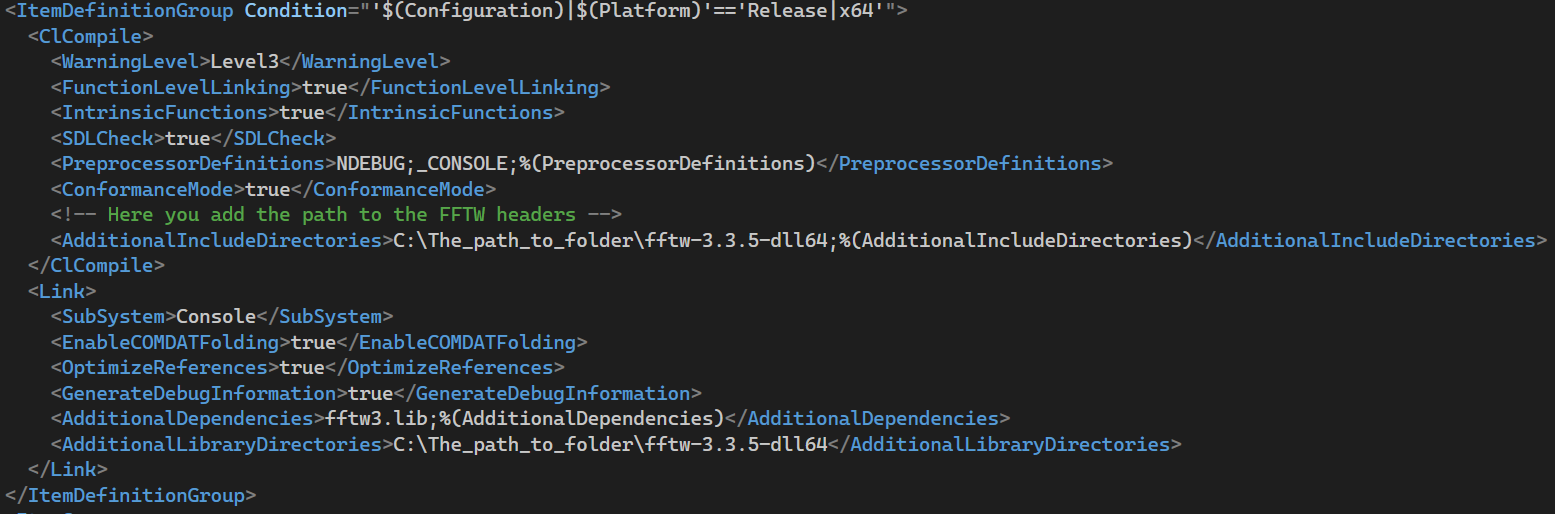
the .vcxproj project file in Visual Studio, as shown in images 4 through 7.
-
It is necessary to ensure that the project is configured with the correct
architecture. In theory, Visual Studio allows switching between 32-bit and 64-bit
configurations by selecting the dropdown menu located in the top bar. It is important
that the architecture of the FFTW library matches the architecture of the project,
meaning if the 32-bit version of FFTW is downloaded, the project must be configured
to compile in x86 (Win32).
Figure 4. Debug Win32 mode configuration.
Figure 5. Release Win32 mode configuration.
Figure 6. Debug x64 mode configuration.
Figure 7. Release x64 mode configuration.
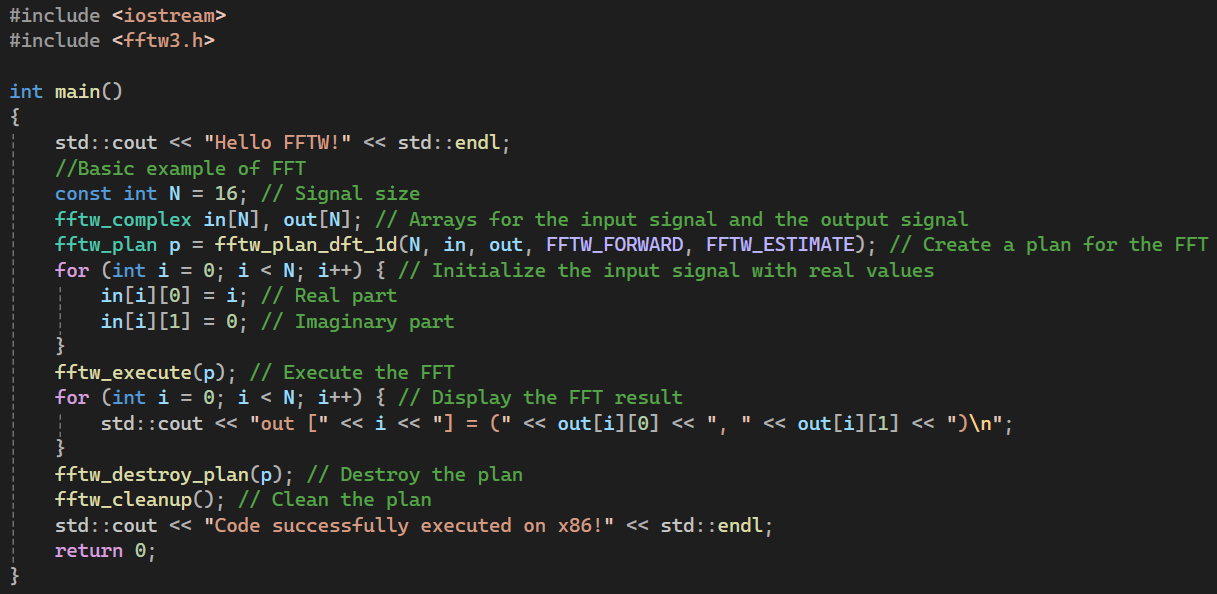
The image shown below is a simple example of code implementing FFTW to compute the Fast
Fourier Transform on a one-dimensional discrete signal. Code explanation:
-
FFTW Library: First, we include the header file fftw3.h, which contains
the definitions of the functions needed to use FFTW.
-
Signal declaration: A signal of size 16 (N = 16) is declared in the vector
in[]. The vector out[] is also declared to store the FFT result.
-
Planning: fftw_plan_dft_1d() generates an FFT plan to transform the
one-dimensional signal. The fftw_plan_dft_1d() function receives the signal size,
the input vector, the output vector, the transform direction (in this case, forward
FFTW_FORWARD), and an estimation option FFTW_ESTIMATE.
-
FFT execution: fftw_execute() is used to perform the Fast Fourier
Transform on the signal.
-
Displaying results: The FFT result is stored in the out[] vector, and
each value is printed.
-
Cleanup: Finally, the plan is destroyed with fftw_destroy_plan() and
fftw_cleanup() is called to free the memory used by FFTW.
Figure 8. Example of C++ code that implements FFTW to perform a Fast Fourier Transform
(FFT) on an input signal.
Results Analysis
The FFT works by decomposing the original signal into a sum of sinusoidal waves of different
frequencies.
The process essentially converts a signal from the time domain to the
frequency domain, allowing the identification of the frequency components that make up the
original signal.
In our specific case, the FFT decomposed the input signal (a sequence
of real numbers from 0 to 15, where the values correspond to discrete points of a real
function in time) into a series of frequencies.
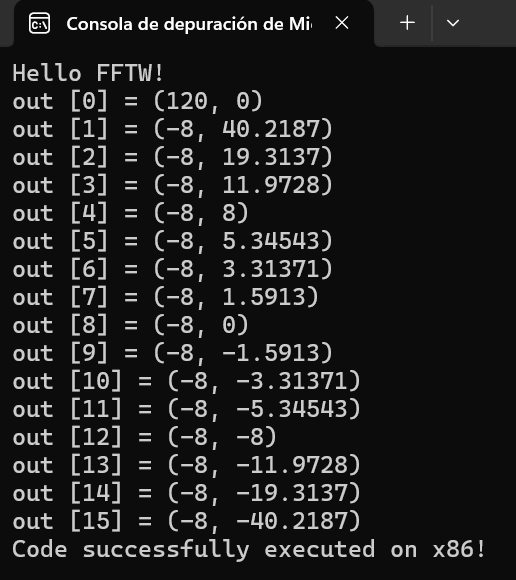
Figure 9. Console output of the FFTW execution, showing the complex output values
obtained after applying the Fast Fourier Transform to a 16-sample input signal in an
x86 environment.
Due to the simplicity of the signal (numbers from 0 to 15), the FFT identified that most of
the energy is concentrated in the low frequencies, which is reflected in the values obtained
in the spectrum.
The result of the FFT is a series of complex values representing the
frequencies present in the original signal. These frequencies are displayed in terms of their
amplitude and phase, allowing us to visualize which frequencies dominate in the input signal.
The complex value out[0] indicates the amplitude of the zero-frequency component, or the
'constant frequency' (DC). In our case, the amplitude of the constant frequency is high due
to the linear nature of the input signal.
The successive values, such as out[1] and
out[2], indicate the amplitude and phase of the higher-frequency components. The real
values correspond to the magnitude of the sinusoidal component, while the imaginary values
indicate the phase of that frequency.
The observed pattern in the results shows that
for a linear signal, the dominant frequency is the constant one (zero frequency), which
explains the high value in out[0].
As we move through the spectrum, the values
tend to decrease, indicating that higher frequencies have less impact on the original signal.
In more complex applications, such as audio analysis or image processing, the FFT can reveal
more interesting frequency components, such as the presence of specific tones in an audio
signal or repetitive patterns in an image.
Results Analysis
The FFT works by decomposing the original signal into a sum of sinusoidal waves of different
frequencies.
The process essentially converts a signal from the time domain to the
frequency domain, allowing the identification of the frequency components that make up the
original signal.
In our specific case, the FFT decomposed the input signal (a sequence
of real numbers from 0 to 15, where the values correspond to discrete points of a real
function in time) into a series of frequencies.
Figure 9. Console output of the FFTW execution, showing the complex output values
obtained after applying the Fast Fourier Transform to a 16-sample input signal in an
x86 environment.
Due to the simplicity of the signal (numbers from 0 to 15), the FFT identified that most of
the energy is concentrated in the low frequencies, which is reflected in the values obtained
in the spectrum.
The result of the FFT is a series of complex values representing the
frequencies present in the original signal. These frequencies are displayed in terms of their
amplitude and phase, allowing us to visualize which frequencies dominate in the input signal.
The complex value out[0] indicates the amplitude of the zero-frequency component, or the
'constant frequency' (DC). In our case, the amplitude of the constant frequency is high due
to the linear nature of the input signal.
The successive values, such as out[1] and
out[2], indicate the amplitude and phase of the higher-frequency components. The real
values correspond to the magnitude of the sinusoidal component, while the imaginary values
indicate the phase of that frequency.
The observed pattern in the results shows that
for a linear signal, the dominant frequency is the constant one (zero frequency), which
explains the high value in out[0].
As we move through the spectrum, the values
tend to decrease, indicating that higher frequencies have less impact on the original signal.
In more complex applications, such as audio analysis or image processing, the FFT can reveal
more interesting frequency components, such as the presence of specific tones in an audio
signal or repetitive patterns in an image.
Results Analysis
The FFT works by decomposing the original signal into a sum of sinusoidal waves of different
frequencies.
The process essentially converts a signal from the time domain to the
frequency domain, allowing the identification of the frequency components that make up the
original signal.
In our specific case, the FFT decomposed the input signal (a sequence
of real numbers from 0 to 15, where the values correspond to discrete points of a real
function in time) into a series of frequencies.
Figure 9. Console output of the FFTW execution, showing the complex output values
obtained after applying the Fast Fourier Transform to a 16-sample input signal in an
x86 environment.
Due to the simplicity of the signal (numbers from 0 to 15), the FFT identified that most of
the energy is concentrated in the low frequencies, which is reflected in the values obtained
in the spectrum.
The result of the FFT is a series of complex values representing the
frequencies present in the original signal. These frequencies are displayed in terms of their
amplitude and phase, allowing us to visualize which frequencies dominate in the input signal.
The complex value out[0] indicates the amplitude of the zero-frequency component, or the
'constant frequency' (DC). In our case, the amplitude of the constant frequency is high due
to the linear nature of the input signal.
The successive values, such as out[1] and
out[2], indicate the amplitude and phase of the higher-frequency components. The real
values correspond to the magnitude of the sinusoidal component, while the imaginary values
indicate the phase of that frequency.
The observed pattern in the results shows that
for a linear signal, the dominant frequency is the constant one (zero frequency), which
explains the high value in out[0].
As we move through the spectrum, the values
tend to decrease, indicating that higher frequencies have less impact on the original signal.
In more complex applications, such as audio analysis or image processing, the FFT can reveal
more interesting frequency components, such as the presence of specific tones in an audio
signal or repetitive patterns in an image.
Conclusions
The success in implementing FFTW not only highlights its efficiency in handling the FFT but
also its potential in future scientific and development projects.
From signal analysis
in fields such as physics and engineering, to its use in image processing, data compression,
system simulation, and trend prediction in finance, FFTW will continue to be an essential tool.
Its ability to work with different data sizes and hardware configurations makes it a versatile
option that will undoubtedly be integrated into innovative projects across various areas of
knowledge and industry.
It is safe to say that FFTW will continue to evolve, providing
fast and efficient solutions in the ever-changing landscape of technology.
Implementing
the FFTW library in C++ allowed firsthand experience of the flexibility and power this tool
offers. From the initial setup to the successful execution of the program, challenges were
overcome thanks to the clear documentation of the library and the developer community that
has contributed to its evolution.
The implementation itself gave us the opportunity to
appreciate how a tool like FFTW facilitates working with large volumes of data by performing
calculations efficiently and accurately.
Moreover, it deepened our understanding of
the importance of using optimized libraries designed to fully leverage hardware resources,
especially in scientific and engineering applications.
Bibliography and Resources
The official FFTW website is the best
starting point for obtaining direct and up-to-date information about this powerful library.
From downloading versions to accessing detailed technical documentation, this site offers all
the resources needed for those looking to implement FFTW in their projects.
For those
who wish to dive deeper into the library, the
official FFTW manual provides detailed examples and technical explanations on how to
fully utilize the library’s capabilities. From installation to advanced implementation, this
manual is an indispensable tool.
FFTW has been the subject of study in various
scientific research papers. Among the most relevant are publications that explain its
architecture and the algorithms it uses to achieve the efficiency it is known for. It is
recommended to explore studies by Matteo Frigo and Steven G. Johnson, the creators of FFTW,
who have published numerous articles in scientific journals detailing the inner
workings of the library.
The official FFTW page provides
code examples for implementing FFTW in different languages, with C and C++ being the most
common. These examples allow developers to quickly start using the library in their projects.
On platforms such as
Stack Overflow and GitHub, there are active
communities discussing FFTW, providing solutions to common problems and sharing code examples to implement
FFTW in specific projects.
There are online
tutorials that explain in a didactic way how to install and configure FFTW, as well as how to optimize
its use in projects. It is recommended to search for courses and videos on platforms such as
YouTube, Coursera, or Udemy to gain a visual and practical understanding of its use.